绪论

XiaoXianYue原创2024年5月16日大约 5 分钟

1. 什么是数据结构？

1.1 数据结构的定义

基本定义：

数据（Data）：描述客观事物的数和字符的集合。
- 信息的载体
- 对客观事物符号化的表示
- 能够被计算机识别存储和加工
数据元素（Data element）：作为数据的基本单位。也可以称为元素，记录，结点或定点。
- 一个数据元素可由若干个数据项组成。
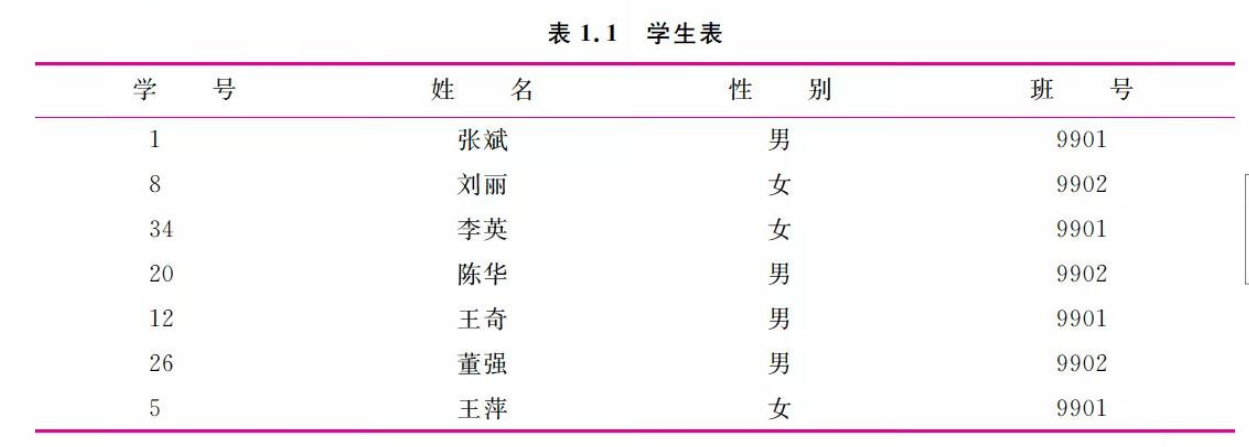
- 如：0003 李明男 2001/03/02是李明的基本信息，也是由若干个数据项组成的数据元素。
数据项（Data item)具有独立含义的数据最小单位，也称为字段和域。
- 数据 > 数据结构 > 数据项，就像学生表 > 个人记录 > 学号姓名…
数据对象（Data Object）性质相同的数据元素的集合，是数据的一个子集。\
- 字母字符数据对象是集合C={'A','B','C'...}
数据结构: 数据元素不是孤立存在的，他们存在着某种关系，数据元素相互之间的关系称为结构。是指相互之间存在一种或多种特定关系的数据元素集合。或者说，数据结构是带结构的数据元素的集合。

数据结构通常也包括以下两方面：

逻辑结构。有数据的逻辑关系构成。
存储结构。数据元素及其关系在计算机存储的表示，也称为数据的物理结构。

1.2 逻辑结构

1.2.1 逻辑结构的表示

图表和二元组。

图表

图形中每一个数据节点对应着一个元素，两结点之间的箭头代表了他们的相邻关系。如下就是上面这个图表的逻辑结构：

二元组表示

一个二元组如下所示：

B=(D,R)

其中B是一种数据逻辑结构，由数据元素的集合D以及D上二元关系的集合R所组成。

对于二元表中相邻的<x,y>，x为y的直接前驱元素，y为x的直接后继元素。

如果一个元素没有前驱元素，则称为开始元素；没有后继元素，则为终端元素。

例子：

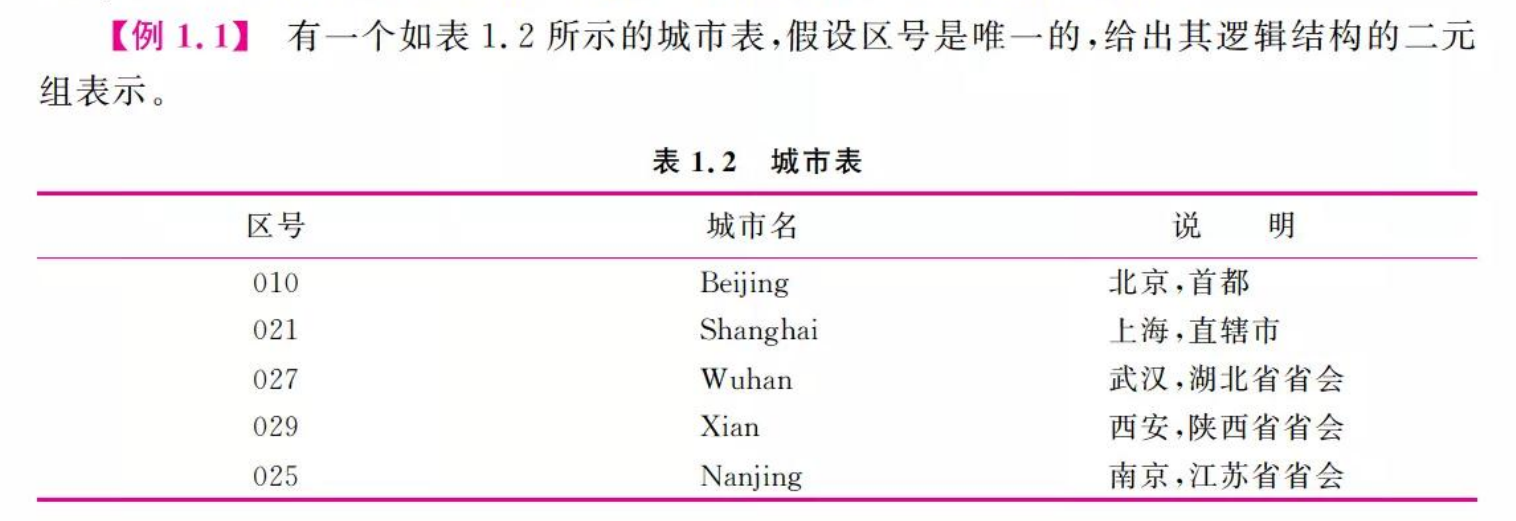
B = {D，R}

D = {010 , 021 , 027 , 029 , 025}

R = { r }

r = {<010, 021> , <021,027>, <027,029>,<029,025>}

1.2.2 逻辑结构的类型

集合

集合（set）是指数据元素之间除了“同属于一个集合”的关系以外别无其他关系。

线性结构

线性结构是指该结构中数据元素之间存在一对一的关系。其特点是开始元素和终端元素都是唯一的，其余元素只有一个前驱元素和后继元素。

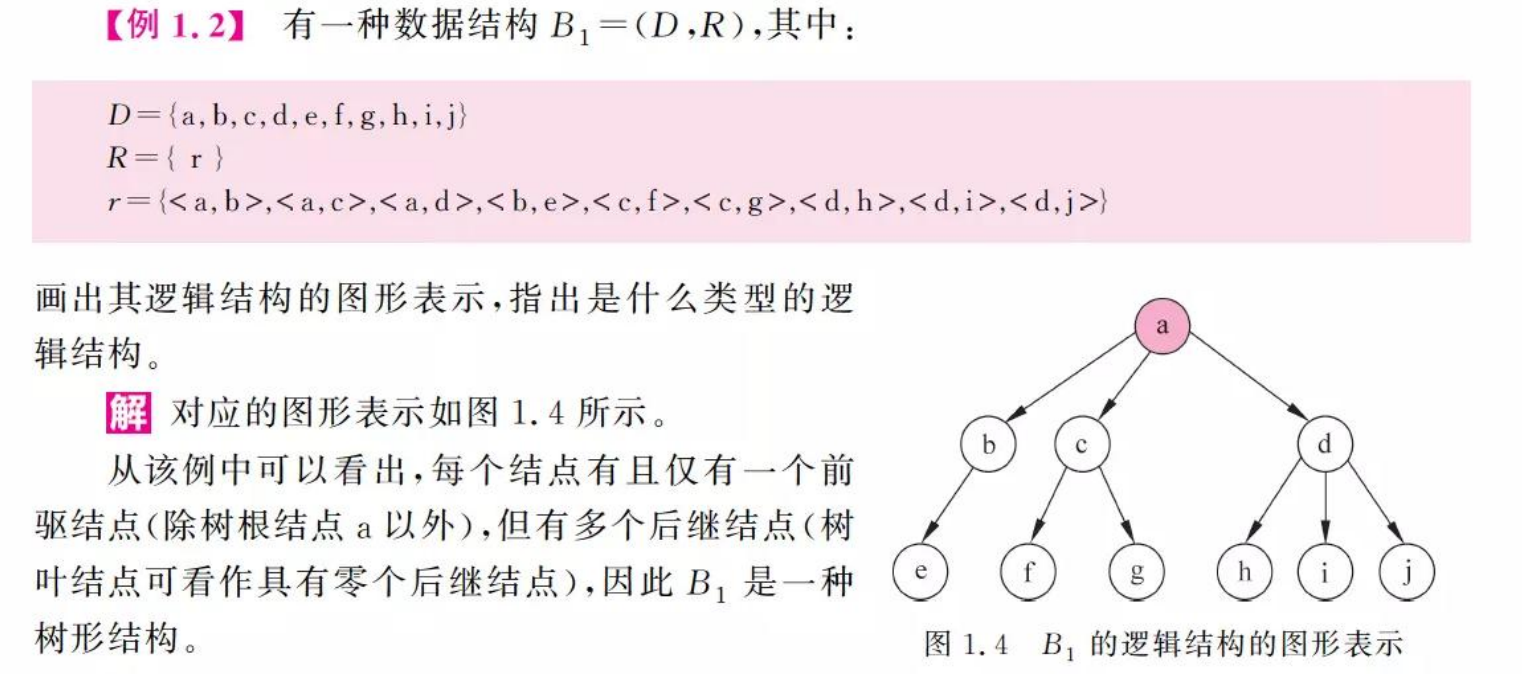
树形结构

树形结构是指该结构中的数据元素之间存在一对多的关系。它的特点是除了开始元素以外，每个元素有且仅有一个前驱元素，除了终端元素以外，每个元素有一个或多个后继元素。

例子：

图形结构

是指该结构中的数据元素之间存在多对多的关系。其特点是每个元素的前驱元素和后继元素的个数可以是任意的，因此图形结构可能没有开始元素和终端元素。

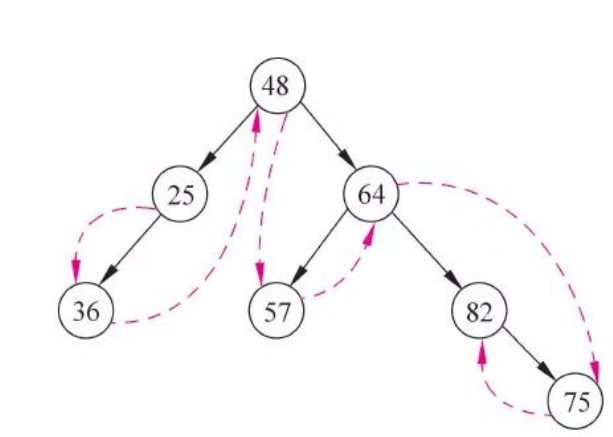
树形结构和图形结构统称为非线性结构。该结构中的元素存在一对多或者多对多的关系。

树形结构是特殊的图形结构，图形结构是特殊的树形结构。

1.3 存储结构

1.3.1 顺序存储结构

采用一组连续的存储单元存放所有的数据元素。

3. 算法分析

3.1 算法的时间性能分析

例题：

计算数组的元素和:

int sumArray(int arr[], int n) {
    int sum = 0;
    for (int i = 0; i < n; i++) {
        sum += arr[i];
    }
    return sum;
}
//O(n)

查找数组中的最大元素:

int findMax(int arr[], int n) {
    int max = arr[0];
    for (int i = 1; i < n; i++) {
        if (arr[i] > max) {
            max = arr[i];
        }
    }
    return max;
}
//O(n)

冒泡排序:

void bubbleSort(int arr[], int n) {
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}
//O(n^2)

线性搜索:

int linearSearch(int arr[], int n, int x) {
    for (int i = 0; i < n; i++) {
        if (arr[i] == x) {
            return i;
        }
    }
    return -1;
}
//O(n)

二分搜索:

int binarySearch(int arr[], int l, int r, int x) {
    while (l <= r) {
        int m = l + (r - l) / 2;
        if (arr[m] == x) {
            return m;
        }
        if (arr[m] < x) {
            l = m + 1;
        } else {
            r = m - 1;
        }
    }
    return -1;
}
//

递归计算斐波那契数:

int fibonacci(int n) {
    if (n <= 1) return n;
    return fibonacci(n - 1) + fibonacci(n - 2);
}
//

插入排序:

void insertionSort(int arr[], int n) {
    int i, key, j;
    for (i = 1; i < n; i++) {//n
        key = arr[i];
        j = i - 1;
        while (j >= 0 && arr[j] > key) {//J
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        arr[j + 1] = key;
    }
}
//O(n^2)

选择排序:

void selectionSort(int arr[], int n) {
    int i, j, min_idx;
    for (i = 0; i < n-1; i++) {//n-1
        min_idx = i;
        for (j = i+1; j < n; j++)//n-i-1
            if (arr[j] < arr[min_idx])
                min_idx = j;
        int temp = arr[min_idx];
        arr[min_idx] = arr[i];
        arr[i] = temp;
    }
}
//O(n^2)

计算字符串的长度:

int stringLength(char str[]) {
    int length = 0;
    while (str[length] != '\0') {
        length++;
    }
    return length;
}
//O(n)

快速排序:

void quickSort(int arr[], int low, int high) {
    if (low < high) {
        int pi = partition(arr, low, high);
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}
//