图
1. 图的基本概念
1.1 图的定义
G=(V,E)
V:顶点(数据元素)的有穷非空集合
E:边的有穷集合
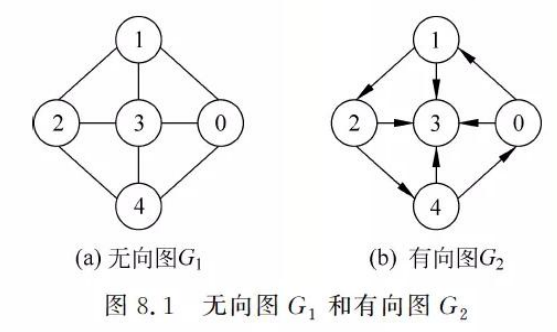
1.2 图的基本术语
- 无向图中:端点和邻接点
有向图中:起始端点和终止端点;出边邻接点和入边邻接点
- 顶点的度,出度和入度
一个顶点所关联的边的数目称为顶点的度。有向图里分出度和入度。
如果一个图中有n个顶点和e条边,每个顶点的度为di(0<=i<=n-1),则有:
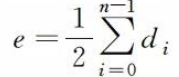
也就是说一个图中所有顶点的度之和等于边数的两倍.
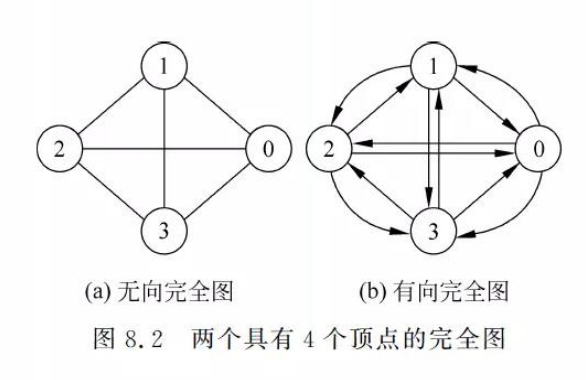
- 完全图
无向图每个顶点之间都存在这一条边;有向图每个顶点之间都存在着双向边.
- 稠密图和稀疏图
字面意思
- 子图

- 路径和路径长度,简单路径
- 回路和环
开始点和结束点是同一个顶点
- 连通,连通图和连通分量

- 强连通图和强连通分量

怎么把非强连通图的强连通分量找出来?

- 权和网

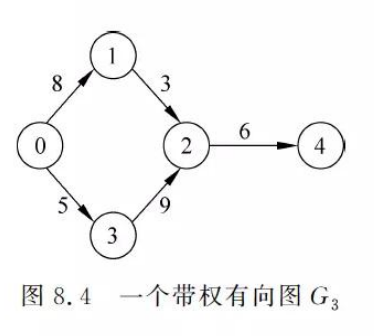
2. 图的存储结构和基本运算算法
2.1 邻接矩阵存储方法
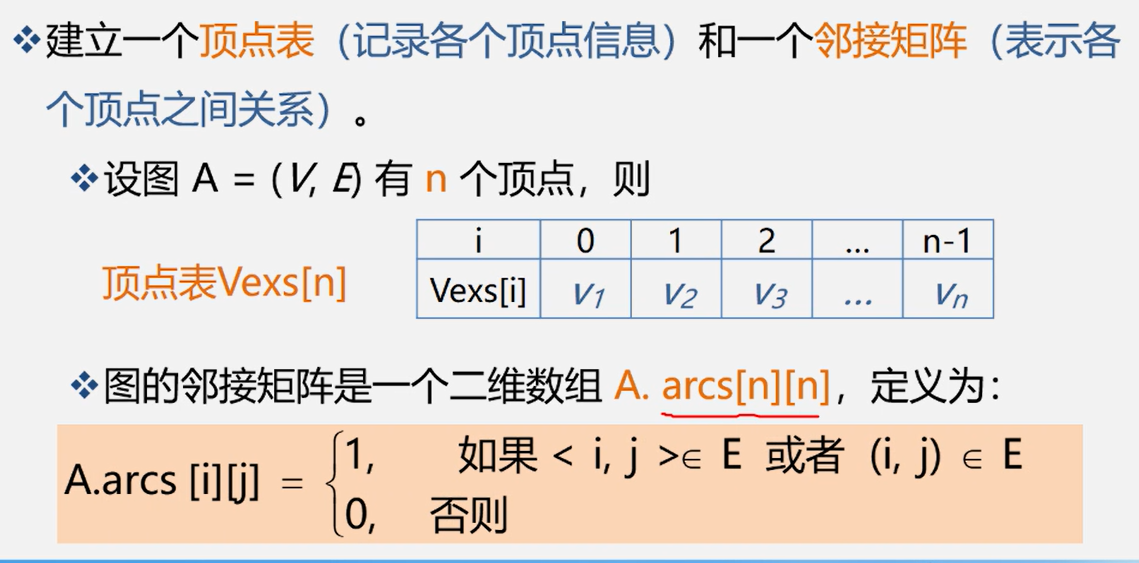
2.1.1 无向图的邻接矩阵:

在完全无向图的邻接矩阵中,除了对角线上的元素都是0,其他都是1
2.1.2 有向图的邻接矩阵:
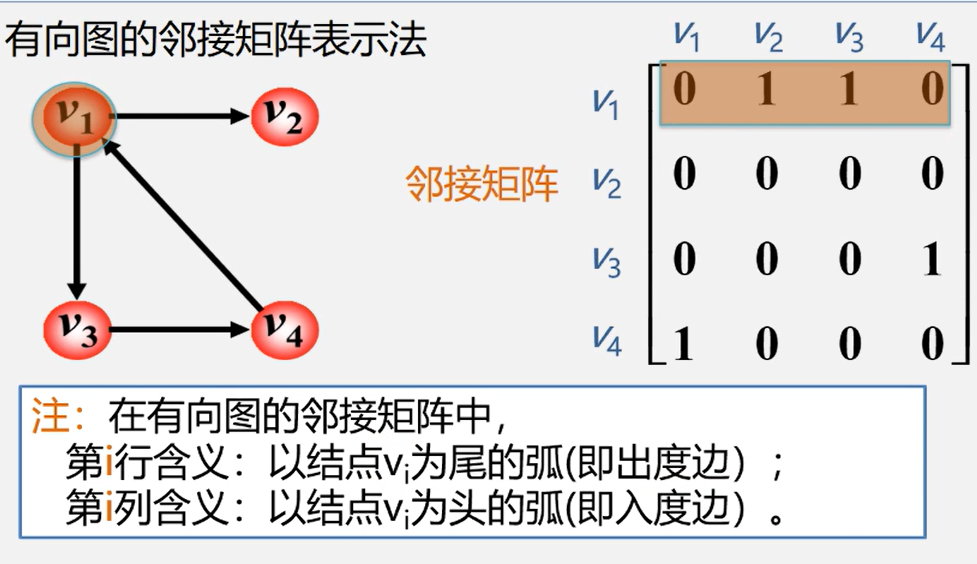
在行处有1的就是该结点发出的箭头(出度边);在列处有1就是该结点收到的箭头(入度边)。

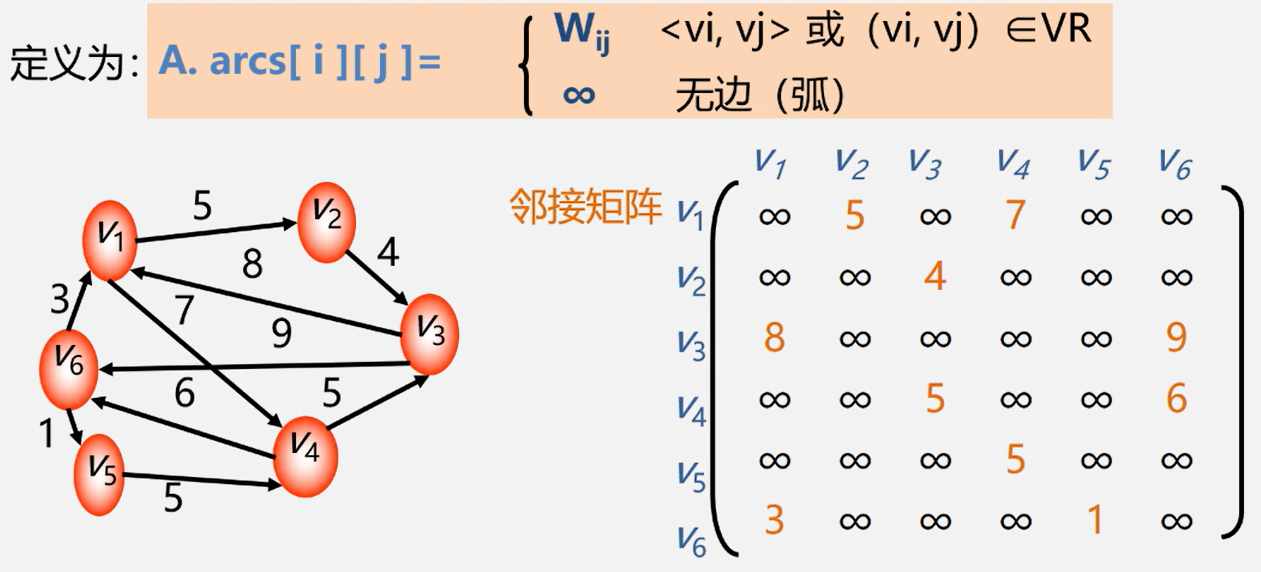
2.1.3 网的邻接矩阵
2.1.4 邻接矩阵的建立

邻接矩阵适合存放稠密图。
图的邻接矩阵是唯一的。
邻接矩阵的空间复杂度是O(n^2)
2.2 邻接表
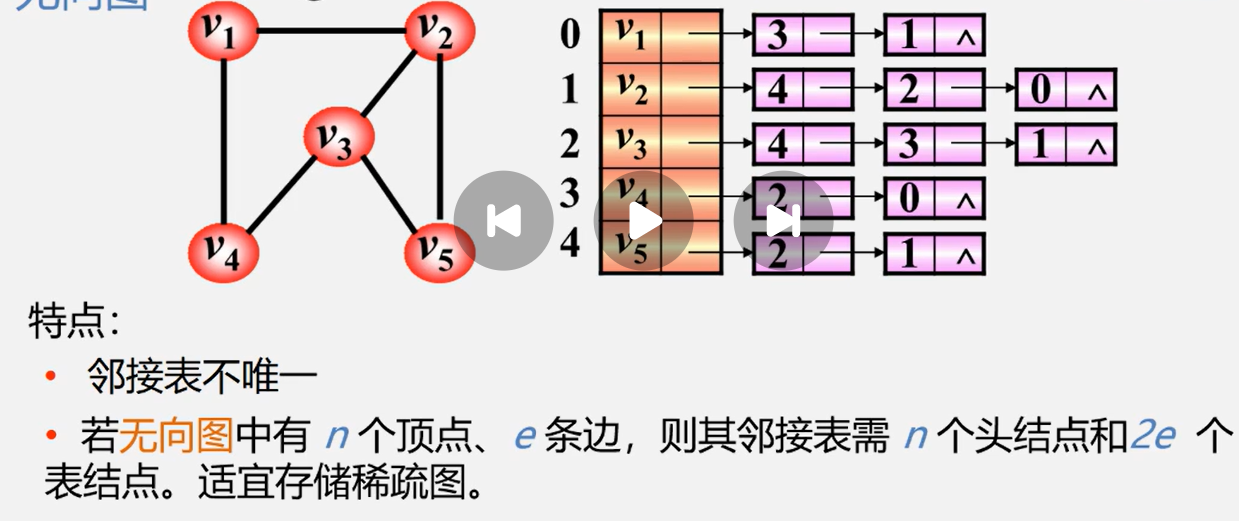
2.2.1 无向图的邻接表
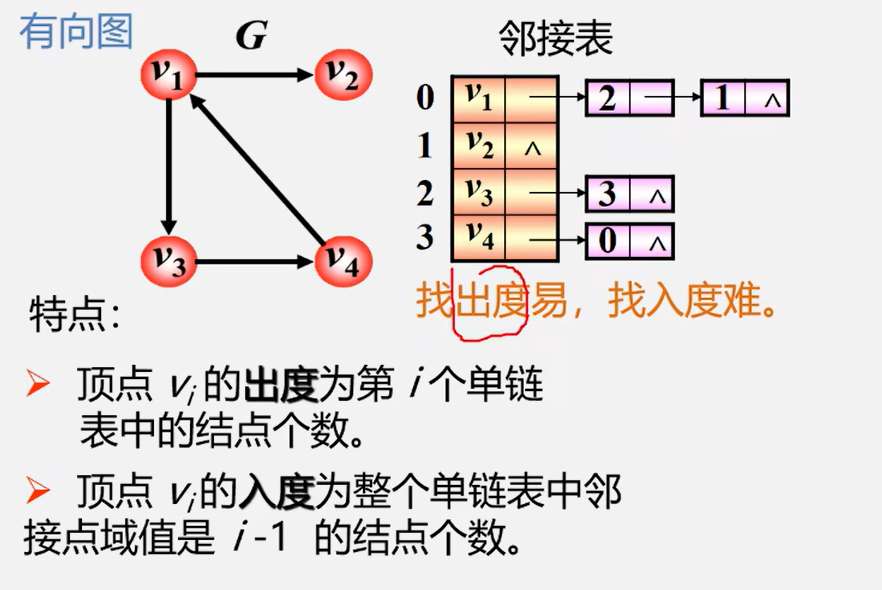
2.2.2 有向图
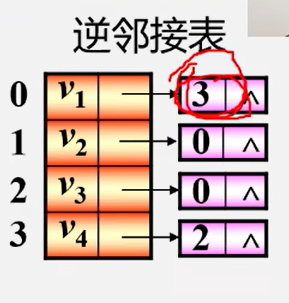
也有逆邻接表

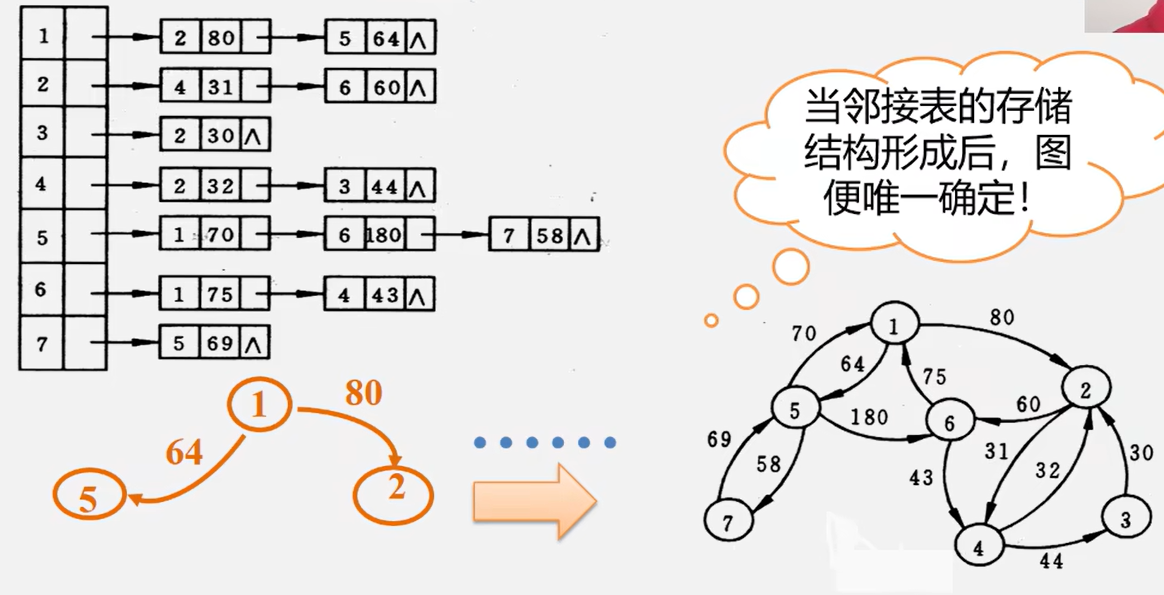
练习:
2.2.3 特点
邻接表适合于稀疏图。
邻接表不唯一
邻接表·的空间复杂度O(n+e)
3.图的遍历
设置辅助数组:

3.1 深度优先搜索(DFS)
3.1.1 连通图
“一条路走到黑”:
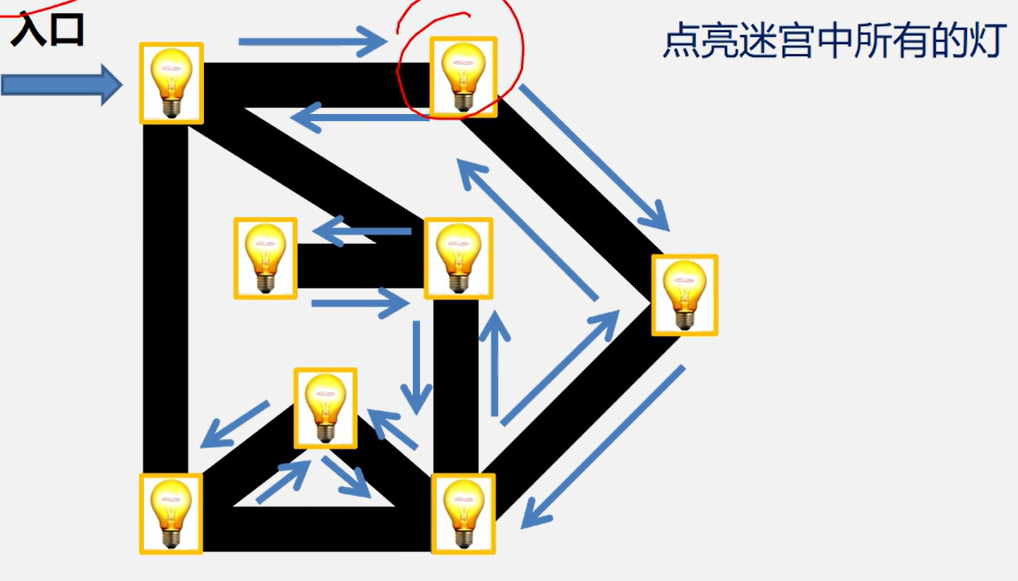
下面例题,自己再做一遍:
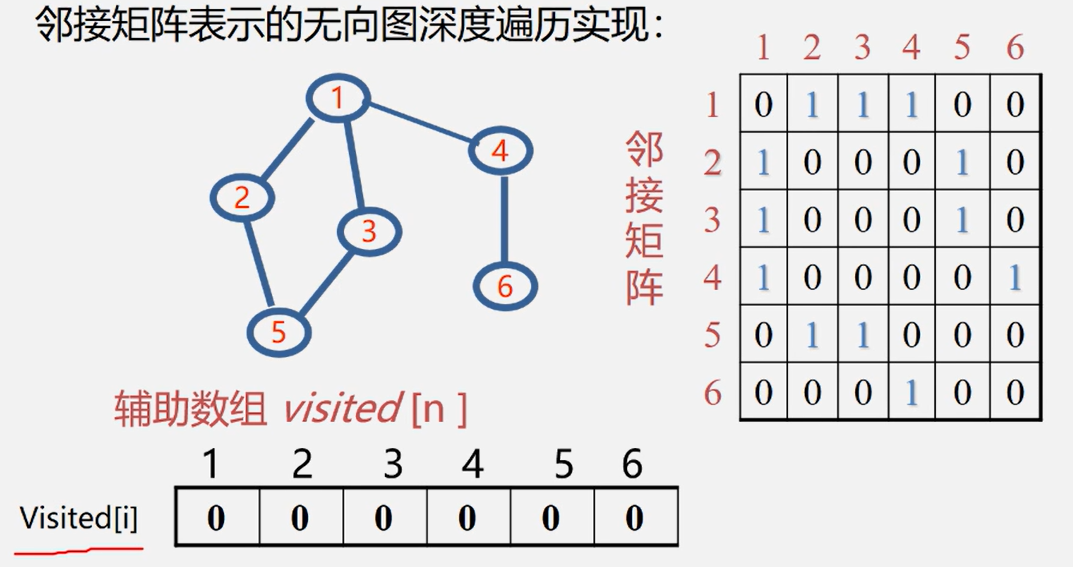
遍历图中每一个顶点都要从头扫描该顶点所在行,时间复杂度为O(n^2)。
但是在邻接表中,时间复杂度为O(n+e),n是头节点数目,e是图中边数。
3.1.2 非连通图
是一样的
遍历完一个连通分量就遍历另一个。
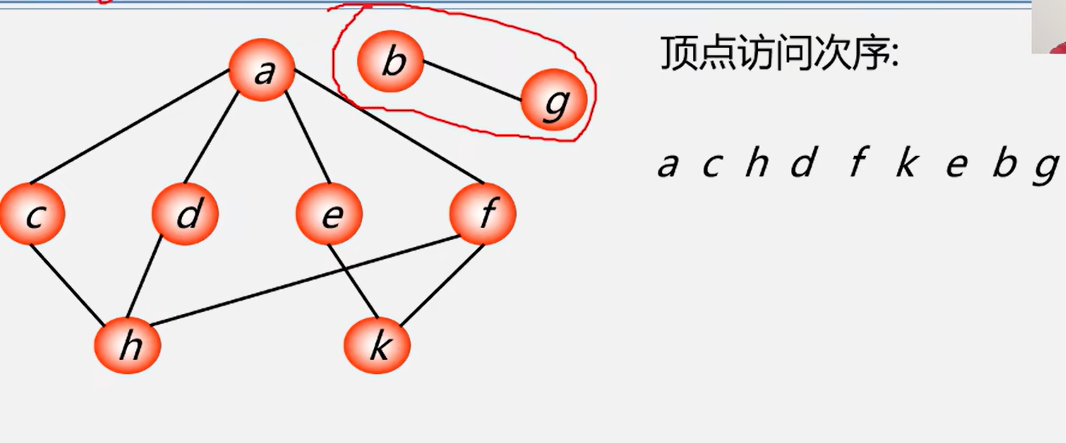
3.2 广度优先搜索(BFS)
- 连通图

- 非连通图
是一样的 分别访问连通分量。
3.2.1 算法实现

3.2.2 效率分析
使用邻接矩阵,O(n^2)
使用邻接表,O(n+e)
3.2.2.1 DFS和BFS的算法效率比较
空间复杂度相同,都是O(n)(借用了堆栈或者队列)
时间效率见上文。都是一样。
4. 图的应用
4.1 最小生成树
4.1.1 生成树
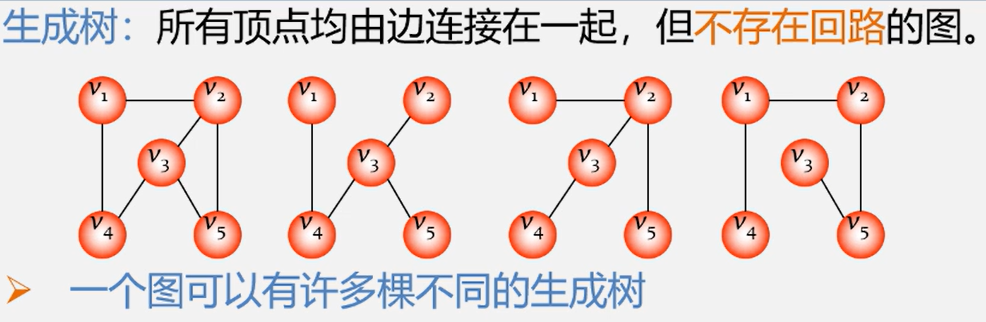
特点
生成树的顶点个数与图的顶点个数相同
生成树是图的极小连通子图,去掉一条边则非连通。
n个顶点的生成树有n-1条边
在生成树中再加一条边必然形成回路。(生成树不能有回路)
任意两个顶点之间的路径是唯一的
4.1.2 最小生成树(MST)
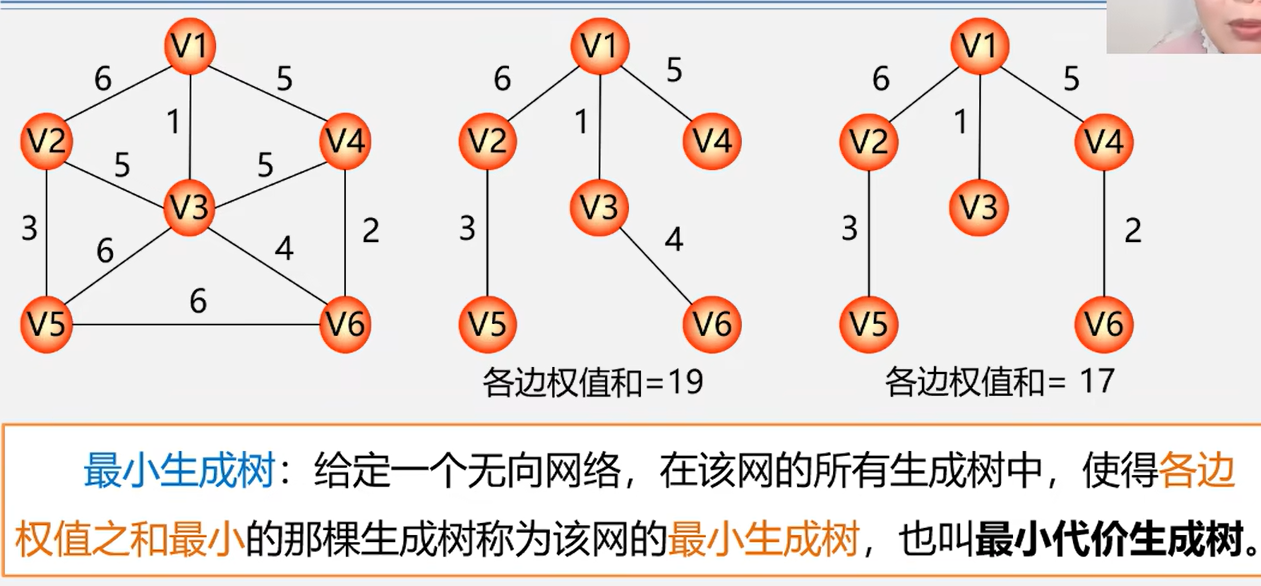
4.1.3 如何构造最小生成树
MST性质解释:
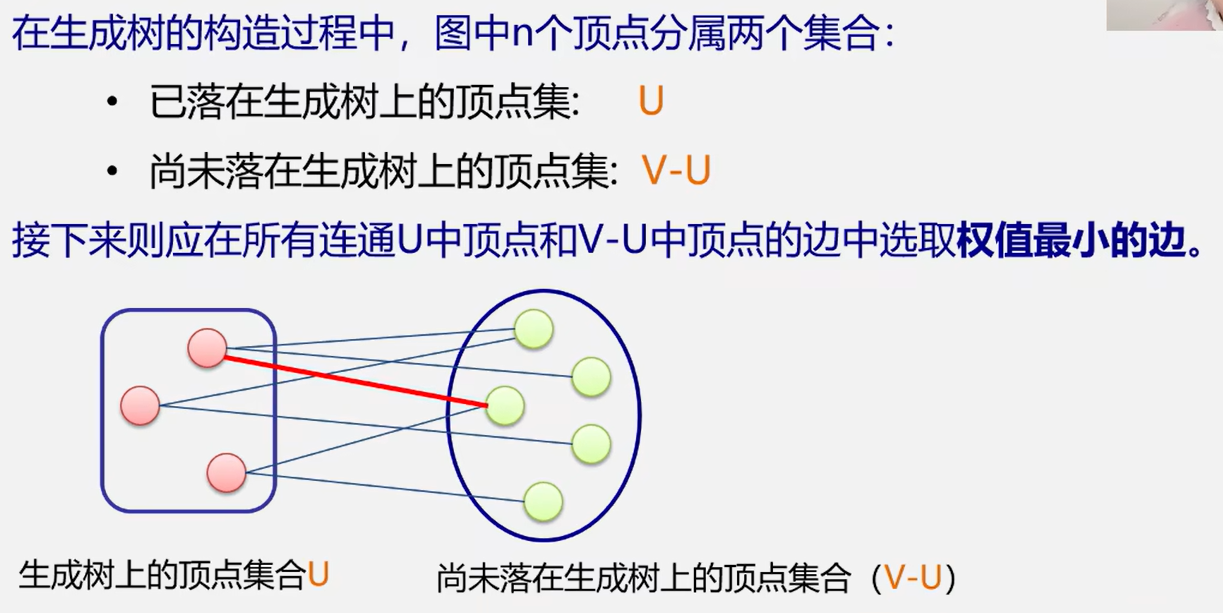
普里姆算法
克鲁斯卡尔算法(出来的生成树有可能不唯一)

对比:
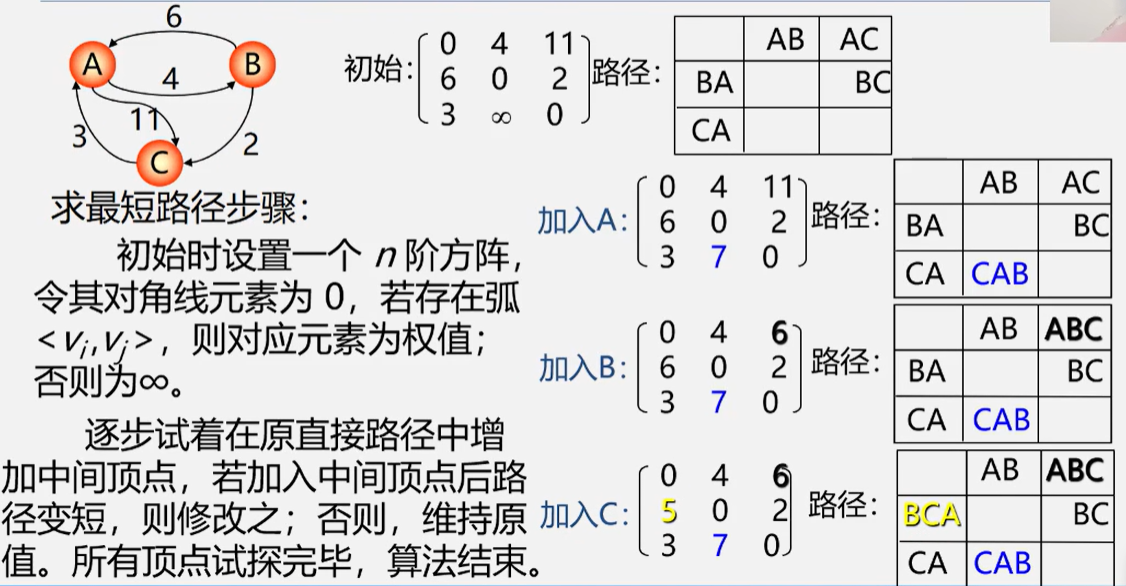
4.2 最短路径问题
在有向网中A点(源点)到达B点(终点)的多条路径中,寻找一条各边权值之和最小的路径,即最短路径。与最小生成树不同,路径上不一定包含n个顶点,也不一定包含n-1条边。
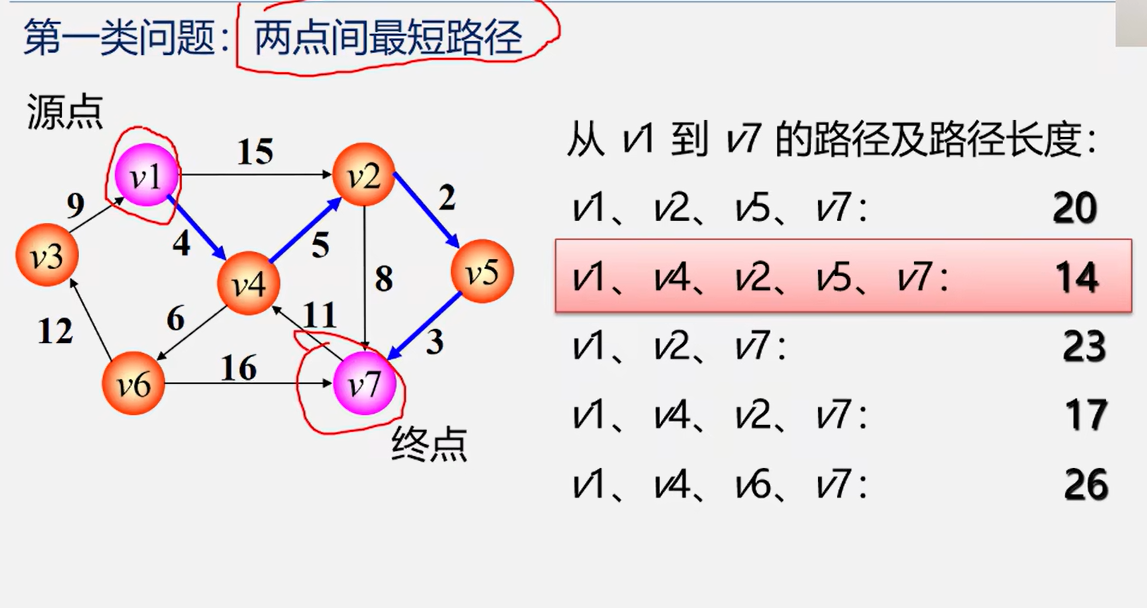
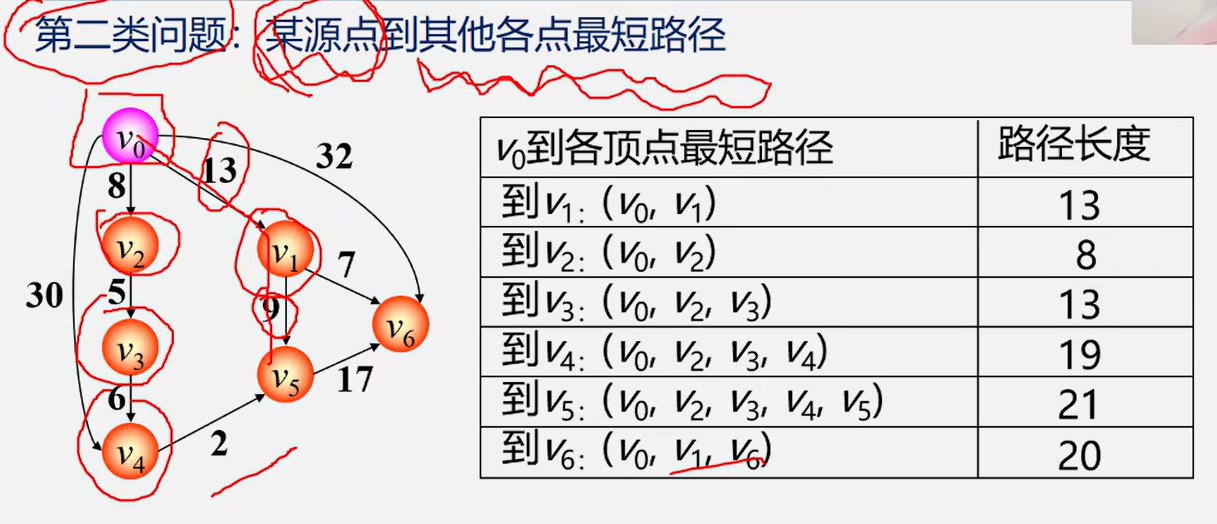
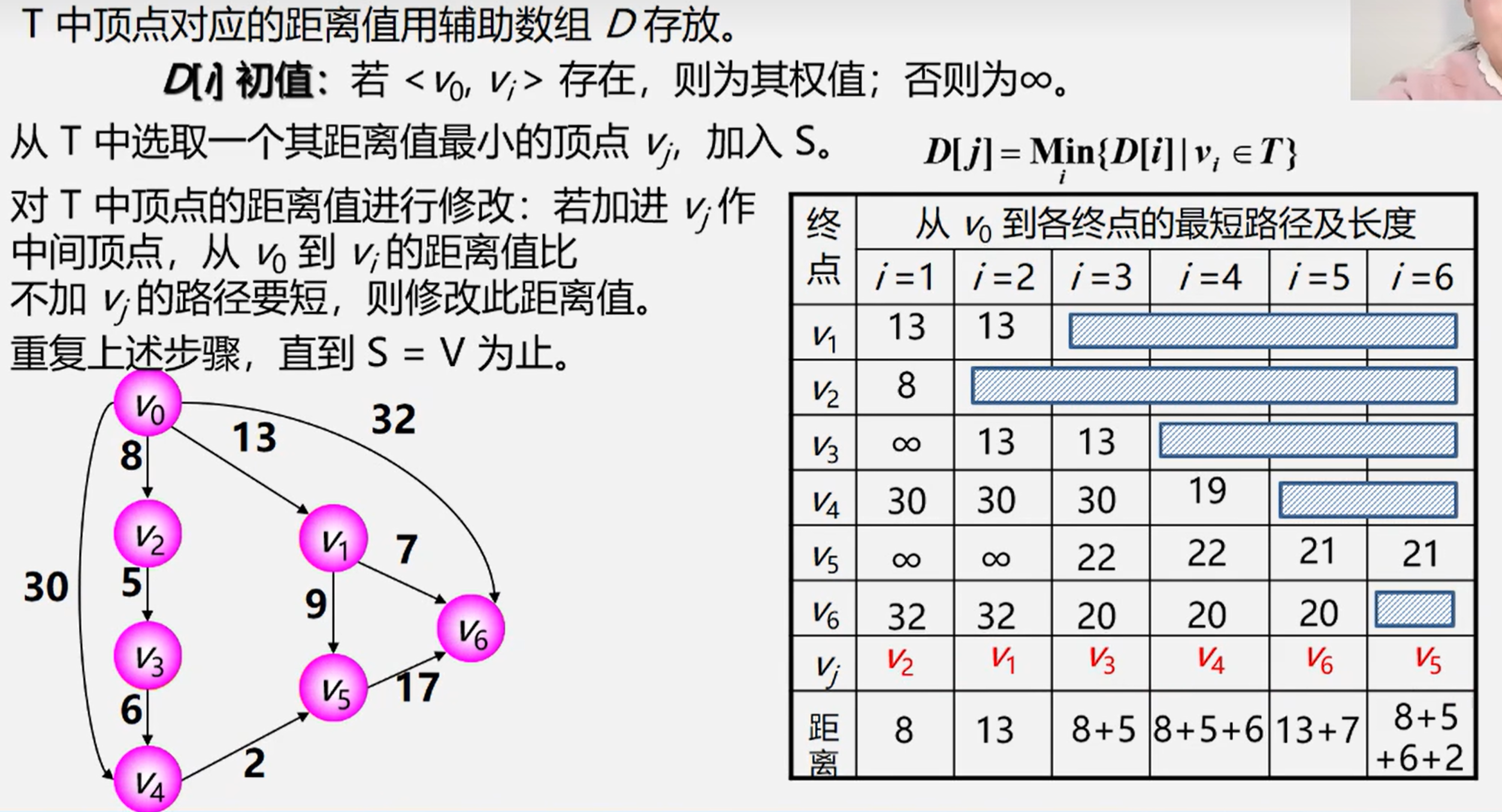
4.2.1 Dijkstra算法(求解单源最短路径)
4.2.2 Floyd(弗洛伊德)算法(所有顶点间得最短路径)